撓性減振材料動剛性設計模型解析與建立

前言
對於超彈性體(橡膠)高度非線性的動態特性(動剛性)，就目前的黏彈性模型(viscoelastic model)、彈塑體模型(elastoplastic model)或疊加模型(generalized Maxwell model)[7]-[10]，都無法完整描述其寬廣頻域反應特性。例如以疊加模型進行擬合，頻率範圍在1 Hz ~ 1e12 Hz間須達40項次方能有效逼近實驗數值[11]。本研究目的即在於整合目前動剛性模型，加入新的連續方程式及參數補足其缺陷，以滿足有限元素分析所需的非線性精度。
動剛性模型解析與整合 
撓性減振元件設計多以超彈性體材料模型為基礎，整合拓撲分析方式，進行初階的結構收斂。超彈性體材料模型在靜態的應力應變關係採用應變能理論，不管是Mooney、Ogden或Treloar…模型[1]-[6]都可以在應變量500%以下時達到與實驗值非常吻合的連續方程式。然而以橡膠為主的超彈性體在動態特性上具有高度的非線性特性，目前的擬合方法多應用數種線性模型疊加，如generalized Maxwell model或是generalized viscoelastic-elastoplastic model，此方法導致方程式項次過多，並具有很長的積分函數，使得有限元素分析時佔用大量的計算時間，例如以generalized Maxwell model代表的阻尼模型的鬆弛函數(relaxation model)，其函式如下：

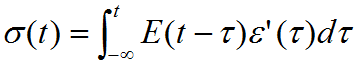(1)

σ為應力，ε' 代表應變變化，E則為鬆弛模數。此方程式在頻域(frequency domain)時，可以簡化為儲存模數與損失模數，但是應用於時域(time domain)牽涉到長時間積分，不利於分析計算。保留鬆弛函數的原始精神，更新為時域的緊弛函數如下：

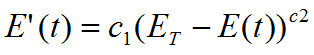    (2)
 
c1與c2為常數係數，ET代表材料在某一應變速度下的目標模數，其意義相同於固定應變下的E∞，模數是隨時間變化，且不僅有鬆弛特性，亦可能有張緊特性。張緊現象存在於應變速度逐漸加大時，通常拉伸或壓縮實驗時較難測量確實數據，但可由拉伸壓縮速度不同時橡膠表現出不同的應力結果得知其存在。假設其模數亦有飽和現象，函式如下：

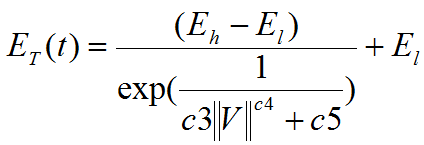   (3)