- 回首頁
- 機械工業雜誌
- 歷史雜誌
摘要:隨著工業4.0與智慧製造時代的來臨,無人搬運車在其中扮演的角色也越來越重要。在現今的半導體封測產業中,無人搬運車已然成為廠區內主要的物流搬運系統。本文探討無人搬運車系統所需導入之最佳車數評估方法,並提出整合式等候線理論模擬模型 (Integrated Queuing Theory and Simulation, IQS)。針對本文所使用之方法,我們以實驗設計分析驗證其可行性與有效性。
Abstract:With the advent of Industry 4.0 and the era of smart manufacturing, the role of Automatic Guided Vehicles (AGV) or Autonomous Mobile Robots (AMR) is becoming more and more important. In today's semiconductor packaging and testing industry, AGVS has become the major material handling system. This article discusses the methods for evaluation of the optimal number of vehicles for the automatic guided vehicles system (AGVS), and proposes an Integrated Queuing Theory and Simulation (IQS) model to generate the optimal fleet size for AGV. Afterward, the technique of design of experiment (DOE) is used to analyze and justify the optimality and feasibility of the model.
關鍵詞:無人搬運車系統、最佳車數、整合式等候線理論模擬模型、模擬驗證
Keywords:Automated guided vehicle system (AGVS), Optimal fleet sizing, Integrated queuing theory and simulation (IQS), Simulation verification and validation
前言
隨著工業4.0的推動,自動化物料搬運系統(Automatic Material Handling System, AMHS)已成為一種趨勢。許多要求無塵等級的自動化工廠,如面板廠或半導體封測廠等紛紛導入無人搬運車系統(Automated Guided Vehicle System, AGVS),以強化整體產線的自動化程度。AGV具有很高的搬運彈性與靈活度,可獨立作業也可規劃一次多台同時運行。在半導體封測廠中,AGV可運行於各個工作站間搬運晶圓盒,能高效且準確地完成搬運作業。雖AGVS可有效協助工廠降低人力成本及提升生產效能,但其系統之導入往往也伴隨許多隨機性變數。AGV車數是影響系統效能的重要因素之一,車數的高估會導致高昂的成本與頻繁的交通堵塞。因此,我們期望透過建立一個有效的數學模型,務實地估計出封測廠所需的車輛數,並利用模擬軟體驗證此數學模型之有效性。
AGVS車數決定相關理論
AGVS所需車數有許多的估算方法。近幾年,較多文獻提及利用數學模型或最佳化方法作估算,其中方法包含等候理論與線性規劃。除此之外,也有學者提出統計的方法,即利用迴歸模型作估算。隨著AGVS之複雜度越來越高,硬體計算能力也越來越強,陸續有文獻提出不同的演算法用以估計AGVS所需的車數。本章節將探討及整理過去文獻所使用之估算方法。
1.等候理論 (Queuing Theory)
在利用等候線模型解決AGVS的車數問題時,車隊數量的決定從估算計劃週期內所需的總車輛行駛時間開始,車輛的總行駛時間包括空載行駛時間、裝載時間、裝載行駛時間以及卸載時間。若事前知道總運送請求,則很容易估算裝、卸載時間與裝載行駛時間,然而,空載行駛時間並不易估算,因其為車輛調度策略的函數。
從等候線系統的角度來看,可以將AGV視為資源,而從一個站點運送物件到另一個站點的運送請求可以視為顧客的到來,因此所需的服務器數量,即車隊數量,取決於顧客到來和代表車輛行駛服務時間的相關參數。其中,任務分配等待時間是指運送請求被分配給車輛前,物件必須等待直到有可用車輛的延遲時間,相當於等待被服務的排隊時間。若在運送請求時有空閒的可用車輛,則任務分配的等待時間為零,根據等候線理論可以估計任務分配的等待時間。
Koo等人[1]、Raman等人[2] 與Tu等人[3] 皆利用運送請求率、裝卸載時間、站點間的行駛時間等參數計算車輛完成運送任務的服務時間,作為AGVS所需車輛數的下限。此下限表示若要在計劃週期內完成系統中的所有運送請求或者使系統處於交通密度不超過1的穩定狀態下,至少必須具備的AGVS車數,也等於所需車數的初始值。運算出所需車輛數的下限後,則可再利用隊列模型的理論獲得等待運送的排隊時間、車輛利用率與在製品數 (Work in process, WIP) 等參數,並且檢驗運送任務的等待時間是否滿足在預定義的時間之內,以維持工廠內期望最佳生產量與產品週期等績效表現。反之,則再增加AGV使系統後重新檢驗至滿足期望目標,其為最佳車輛數,圖1呈現使用等候線模型決定車數的輸入參數與流程。
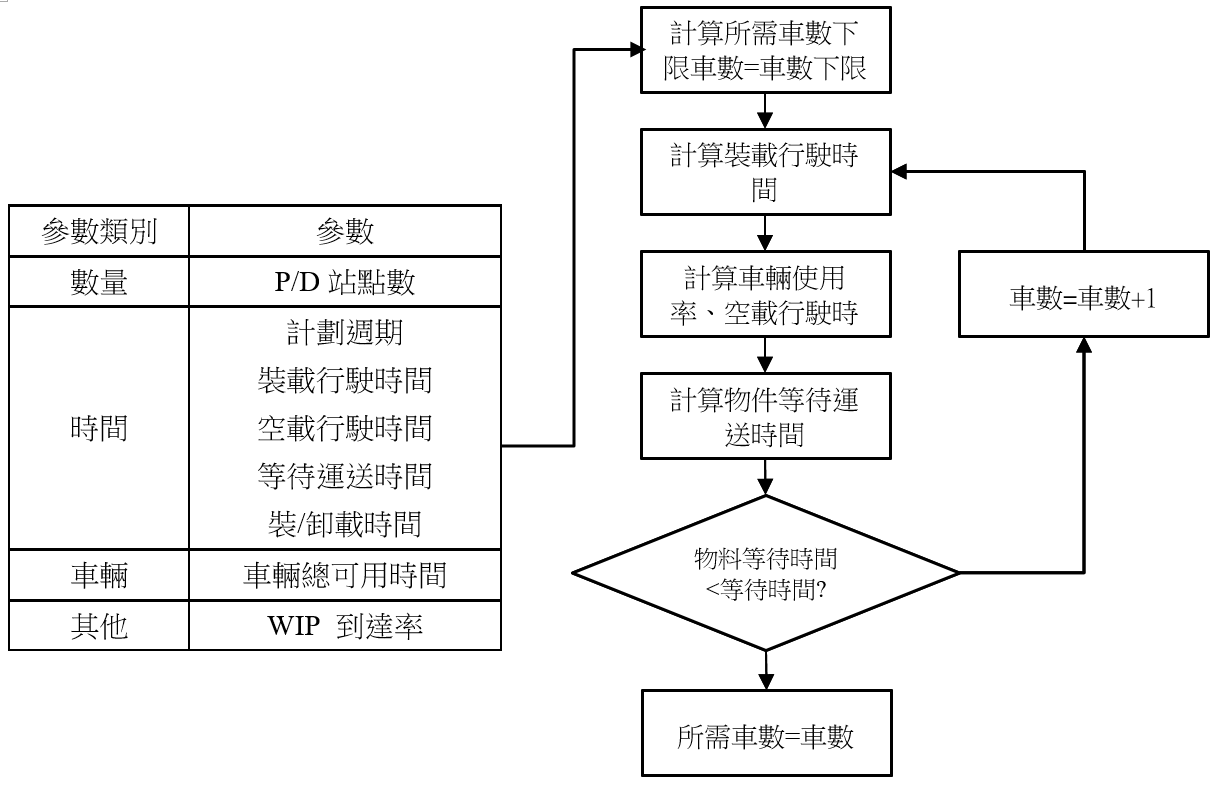
圖 1 等候線模型方法流程範例
更完整的內容歡迎訂購 2022年08月號 (單篇費用:參考材化所定價)